Trigonometri (Kel. 4)

 

KELOMPOK 4

TRIGONOMETRI

Trigonometri adalah cabang ilmu dalam Matematika yang mempelajari hubungan antara sisi dan sudut pada segitiga.

Hubungan itu biasanya dinyatakan sebagai perbandingan sinus, kosinus, dan tangen.

JENIS-JENIS TRIGONOMETRI

Jenis-Jenis Trigonometri Perbandingan dasar trigonometri terdiri

dari sinus, kosinus, dan tangen. Dari perbandingan tersebut, akan muncul perbandingan lain, seperti kosekan, sekan, dan kotangen.

 

Apa sih maksud perbandingan- perbandingan tersebut? Untuk lebih jelasnya, perhatikan gambar segitiga siku-siku berikut.

 

 

Dengan:

 

x = AB = panjang sisi mendatar segitiga;

y = BC = panjang sisi tegak segitiga;

r = AC = panjang sisi miring atau sisi terpanjang

segitiga; dan

= besarnya sudut yang dibentuk oleh sisi-sisi segitiga.

 

sinus

Sinus atau bisa disingkat sin adalah perbandingan antara panjang sisi di depan sudut dan panjang sisi miring. Secara matematis, dirumuskan sebagai berikut.

 

TANGEN

Tangen atau biasa disebut tan adalah perbandingan antara panjang sisi di depan sudut dan panjang sisi di samping sudut. Secara matematis, dirumuskan sebagai berikut.

KONSINUS

Kosinus atau biasa disebut cos adalah perbandingan antara panjang sisi di samping sudut dan panjang sisi miring.

Secara matematis, dirumuskan sebagai berikut.

KOSEKAN

Kosekan adalah perbandingan antara panjang sisi miring segitiga dan panjang sisi di depan sudut. Dengan kata lain, kosekan merupakan kebalikan dari sinus. Secara matematis, dirumuskan sebagai berikut.

 

SEKAN

Sekan adalah perbandingan antara panjang sisi miring segitiga dan panjang sisi di samping sudut. Dengan kata lain, sekan merupakan kebalikan dari kosinus. Secara matematis, dirumuskan sebagai berikut.

KOTANGEN

Kotangen adalah perbandingan antara panjang sisi di samping sudut dan panjang sisi di depan sudut. Dengan demikian, kotangen merupakan kebalikan dari tangen yang secara matematis, dirumuskan sebagai berikut.

 

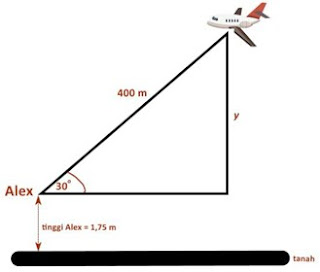
sin α = y/400

& sin 30∑ = y/400  

y = 200 m

Oleh karena nilai y = 200 m, maka ketinggian pesawat

dari permukaan tanah bisa dinyatakan sebagai berikut.

ketinggain pesawat = 200 + tinggi Alex

=200 + 1,75

= 201,75 m

Jadi, ketinggian pesawat dari permukaan tanah adalah 201,75 m.

 

3. Terdapat segitiga ABC siku-siku di B dan besar sudut C adalah 60°. Tika

panjang AC = 12 cm, maka tentukanlah

panjang:

(a) AB

(b) BC

Tawaban:

(a) sin sin 60° = ACBC

3√2 = AB12

AB = 12 ×3√2

AB = 63-√

(b) cos cos 60° = BCAC

12=AB12

AB = 12×12

AB = 6

 

4. Bila A + B = phi/3 dan cos A cos B = 5/8,

maka berapa cos (A - B)?

Jawaban:

Cos (A + B) = cos phi/3

Cos A cos B - sin A sin B = ½

5/8 - sin A sin B = ½

Sin A sin B = 1/8

Maka:

Cos (A - B) = cos A cos B + sin A sin B

Cos (A - B) = COS A cos B + sin A sin B

Cos (A -B) = 5/8 + 1/8

Cos (A - B) = ¾